I contributi di Pascal in campo matematico
La "lumaca" di Pascal e lo studio delle coniche
Pascal era un prodigio matematico. Anche suo padre aveva una notevole inclinazione per la matematica; la "lumaca di Pascal" prende appunto il nome dal padre Etienne. Questa curva era nota già agli antichi come la "concoide del cerchio", ma Etienne Pascal ne fece uno studio così approfondito che da allora porta il suo nome.
Data una curva piana C ed un punto O del suo piano, si dice concoide della curva C (dove C è detta base della concoide) rispetto ad O (polo della concoide) la curva ottenuta in questo modo: sopra una retta generica condotta da O si riporta, a partire dall'intersezione M di tale retta con C, dall'una e dall'altra parte di M, un segmento MP = MQ di lunghezza l assegnata (intervallo della concoide). La concoide è il luogo dei punti P e Q al variare della retta nel fascio di centro O. In particolare, se la curva C è una circonferenza, si ha la cosiddetta "lumaca di Pascal" o semplicemente chiocciola. Assumendo come asse x il diametro passante per O e come asse y la tangente al cerchio in O, essa ha equazione cartesiana:
(x2+y2 - 2ax)2 - L2(x2 - y2) = 0
Per L = 2a (dove 2a Š il diametro della circonferenza),
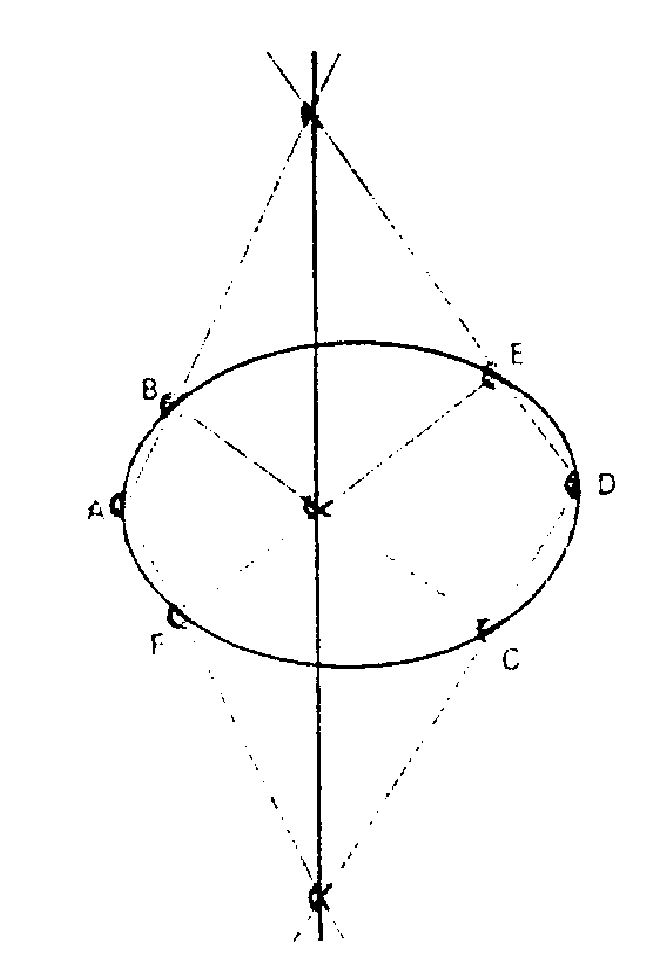
la lumaca di Pascal assume la forma di un cuore e prende perciò il nome di cardiode.A quattordici anni Blaise, insieme al padre, cominciò a partecipare alle riunioni informali della "accademia di Mersenne" a Parigi. Qui conobbe le idee di Desargues e due anni dopo, nel 1640, pubblicò un ESSAY POUR LES CONIQUES che consisteva in un'unica pagina stampata, ma si trattava di una delle più feconde pagine della storia della matematica: conteneva la proposizione, descritta dall'autore come MYSTERIUM HEXAGRAMMATICUM, che da allora è nota come TEOREMA DI PASCAL. Esso afferma che dato un esagono semplice inscritto in una conica, i lati opposti di esso si tagliano in tre punti di una stessa retta (retta di Pascal).Il teorema fu enunciato da Pascal per un comune esagono inscritto in una circonferenza: la generalizzazione fu fatta successivamente nell'ambito della teoria delle coniche. In tale ambito, per esagono semplice, s'intende una figura costituita da sei punti (o vertici) congiunti da sei segmenti (o lati) nello stesso ordine in cui i vertici sono enunciati.

ABCDEF è l'esagono semplice; i lati opposti sono AB; DE; CD; FA; EF.
Il giovane Pascal proseguiva affermando di aver ricavato da questo teorema molti corollari, compresa la costruzione della tangente ad una conica in un punto della stessa.
L'ESSAY inaugurava sotto i migliori auspici la carriera matematica di Pascal, i cui interessi, però, erano dei più vari.
Nel 1654 rivolse nuovamente il suo interesse alla matematica e lavorò a due progetti separati. Uno di questi doveva essere un'
Opera completa sulle coniche, evidentemente una continuazione del piccolo ESSAY che egli aveva pubblicato quasi 15 anni prima; ma quest'opera maggiore sulle coniche non fu mai stampata ed è andata perduta. Leibniz ne vide una copia manoscritta, e gli estratti che ne fece costituiscono ora tutto ciò che c'è rimasto di quest'opera maggiore di Pascal.(Dell'opera minore sulle coniche ci sono rimaste soltanto due copie). Dagli appunti di Leibniz risulta che l'opera completa sulle coniche conteneva una sezione sui Magna Problemata consistenti nel sistemare una data conica in un dato cono di rivoluzione. Il trattato faceva uso di metodi sintetici: infatti, per ragioni che ci sono oscure, non si trovava a suo agio nell'uso dell'algebra simbolica, oppure non si rendeva conto dell'importanza di una buona notazione nella scoperta matematica. Sotto quest'aspetto egli era indietro rispetto ai suoi tempi.
Nel 1658 rivolse l'attenzione allo studio della
cicloide. Essa consiste in una curva descritta da un punto di una circonferenza che rotoli senza strisciare lungo una retta. E' la linea risultante della combinazione di un modo di rotazione e di traslazione e ha la forma di una serie di archi (uno per ogni giro completo).Dopo aver trovato aree, volumi e centri di gravità associati alla cicloide, Pascal propose una mezza dozzina di questioni del genere ai matematici del suo tempo, offrendo premi per la loro soluzione e nominando Roberval come uno dei suoi giudici.
Per la scarsa pubblicità della cosa, furono presentati soltanto due gruppi di soluzioni, che contenevano alcuni errori di calcolo. Perciò Pascal non assegnò alcun premio, tuttavia pubblicò le proprie soluzioni.